What is a convolution?

1. Introduction
2. What Is A Convolution?
3. What Is A Signal?
4. How Does Convolution Work?
5. Signals and Systems
6. Where Do We Use Convolution?
7. Calculating Convolutions
8. Synopsis

Introduction

Convolution is a bit hard to understand at first, or so was the case for me, at least. In this article, I’ll go through what it is, where and why to use it, and how to calculate it, in as high-level language as I can.

What Is A Convolution?

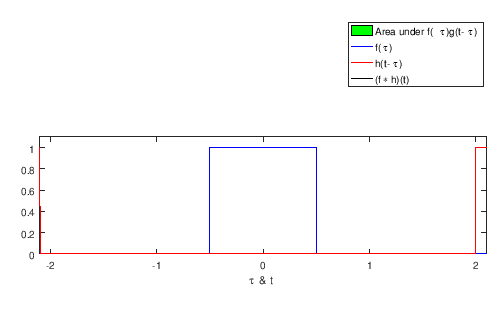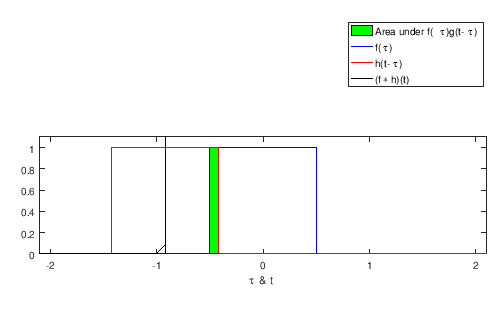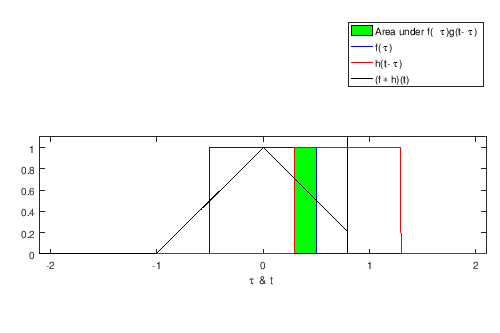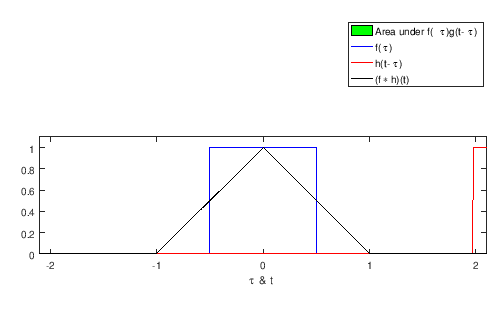
Convolution (operator symbolized as $*$) describes the output of a linear, time-invariant (LTI) system. More specifically, it’s a linear operation between an input signal $x(t)$ (continuous) or $x[n]$ (discrete) and an impulse response $h(t)$ or $h[n]$ respectively, so that we get the desired output signal $y(t)$ or $y[n]$. It is often used for filtering frequencies in the input signal $x(t)$ or $x[n]$.

“What?” I hear you ask…

Basically, we apply a signal on top of another signal (usually a filter-signal on top of a measurement-signal). The signals can be either continuous or discrete. But what is a signal? - well, read on below.

What Is A Signal?

A signal is a function representation of a measurement, living in the n-dimensional space. You can substitute signal for function any time you feel lost, if that helps you grasp the concept. Below are some examples of signals:

• Images - A black-and-white image can be represented as a signal with its independent variables being x, y (coordinates of a pixel), and the dependent variable ($f(x,y)$) being the color of a pixel, in this case a value from 0 to 255. You can imagine, if the image is in color, we get 3 dependent variables (r, g, b) - so we work in a higher-dimensional space.
• Sound - The sound wave can be represented as volume as a function of time (more precisely, audio pressure as a function of time - the pitch is described by the frequency of the wave, but we won’t get into that right now). We might convolve this signal with, say, a high-pass filter (HPF) in order to remove some unwanted frequencies.
• Circuits - The values of current carried through a resistance R can be described as a signal represented as a function of time, $i(t)$.

Example of a continuous signal

Example of a discrete signal

How Does Convolution Work?

The way convolution works can be described simply by the following steps:

1. Reverse one of the two signals (usually the smaller in domain).
2. Shift the reversed signal through time*, from $-\infty$ to $+\infty$.
3. Multiply their values for each point where both of the signals are $\neq 0$.
4. Sum all the above products we get for each shift in time (e.g. $t = 2)$. This is the value of the output signal where its independent variable is equal to the shift in time.

*we use time for simplicity. The independent variable(s) might be something else

The image below illustrates how it works:

Usually, we apply the smaller (in domain) signal on top of the bigger one, with time shift (continuous signals) or increments/steps (discrete signals). The output signal is $\neq 0$ only where the constant signal is defined and around*.

*meaning $\frac{1}{2}$ the length of the reversed signal

Signals and Systems

Signals and Systems is a great chapter on its own, and we will see a lot more of it in the future. For now, think about a system like this:

where $x(t)$ is the input signal, $y(t)$ is the output signal, and the box with the function $F(\cdot)$ is the means of getting the desired output from our input. That combination is a system.

In our case, when we use convolution to get the desired result, we get this instead:

for discrete signals, we get, respectively:

Where Do We Use Convolution?

Where do we not?

But seriously, convolution is the basis of signal processing. It’s used to mix and master audio, apply filters on our pictures on Instagram, change the way movies look and feel (colors, special effects), it’s used in circuit theory, all the way over to processing medical data.

It’s also the base of Convolutional Neural Networks (CNNs), which are a big part of machine learning and especially deep learning, and are used extensively in areas such as computer vision, natural language processing, drug discovery for medical treatment, and many more.

Calculating Convolutions

There are better guides and more qualified people on the internet that can teach you how to calculate convolutions, and you should look it up if you work a lot with signal processing. For the purposes of this guide, a high level overview of how it’s done is enough, as you are likely to use an external library or other tool for the actual calculation process. I still feel, however, that a solid understanding is essential to minimize mistakes and half-assed learning of the fields you might use convolutions in.

We calculate the convolution of two signals as such:

depending on which signal we want to reverse. Notice the equivalence sign between the two equations.

For continuous signals, we have to use integrals instead of sum.

Synopsis

In this article we took a look at convolution, its uses, how we calculate convolutions and we briefly touched on signals and systems, a topic that we’ll take more than a peek on in later articles.

PS: Special thanks to Theodosis Gkamas for helping me with this article.